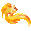На сегодняшний день многие вопросы в теории квантовой физики остаются малоизученными и не дают достаточно полного и логичного объяснения получаемым на практике результатам:
— несоответствие зависимостей частоты и длины волны от температуры;
— отсутствие взаимосвязи между атомами водорода и гелия, а соответственно, между ними и другими элементами таблицы Менделеева;
— наличие довольно сложного и запутанного в объяснениях подхода к вопросу сверхтекучести (в частности, гелия II рода).
Эти и многие другие неосвещённые на сегодняшний день в теоретических выкладках моменты, заставляют искать новые подходы, обеспечивающие полное теоретическое объяснение получаемым на практике результатам.
Один из таких подходов, с точки зрения автора в полной мере согласующийся с основополагающимися теоретическими выкладками родоначальников квантовой физики, и предлагается Вашему вниманию.
Итогом этой работы являются следующие константы (const):
«Ш» = 2,32549 · 10^-4, эВ/градус — универсальная постоянная изменения потенциала (электронвольт) при изменении температуры на один градус (Цельсия или Кельвина);
«М» = 562,311 · 10⁸ , эВ/градус — универсальная постоянная изменения частоты (герц) при изменении температуры на один градус (Цельсия или Кельвина);
Т_иониз¹₁H = 58564 Кº — температура, при которой
атом водорода ионизируется, становясь протоном;
Т_иониз⁴₂He = 31812 Kº температура ионизации атома гелия.

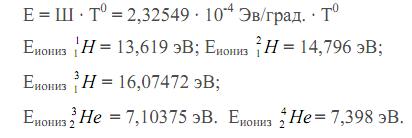
Из учебников физики, с точки зрения изучения атома, мы знаем константу «2п²». В атоме она позволяет определять наибольшее количество электронов на n-ой его оболочке. При этом возникают следующие вопросы:
появляется такое количество электронов на самом деле или это количество квант-состояний электрона (групп электронов), ведь количество электронов у каждого атома различно и зависит от заряда ядра атома. Так у водорода один электрон, у гелия- два, у лития- три и т.д., т.е. у каждого атома — определенное количество (Z) электронов.
При этом, они квантуются группами, или каждый сам по себе, в том числе и внутри групп?
По мнению автора, получившему подтверждение в нижеприводимых расчётах, квантование электронов происходит группами по «z» электронов, и такая группа имеет в атоме 2n²/z квант-состояний с первой по одиннадцатую оболочки и на самой одиннадцатой оболочке.
Это относится ко всем атомам- и с зарядом ядра «z», равным 1, 2, 3 …, и с зарядом 80, 92, 100 и т.д. Это первый из выводов в вышеприведённых рассуждениях, взятый в основу предлагаемого нового метода.
Вторым выводом должно стать признание существования в реальных условиях перехода материальной частицы- электрона, в электромагнитный импульс и наоборот- из электромагнитного импульса, путём «закручивания» энергии она преобразуется в электрон. Зная эти условия, можно осуществить разрыв межмолекулярных связей в экзотермическом режиме, когда процесс распада молекулы происходит не просто без затрат дополнительной энергии, а и с выделением внутренней энергии связей, причём в больших количествах. Именно эти переходы из материального состояния в энергетическое и объясняют свойства гелия II рода — известно, что при определённых условиях он становится сверхтекучим и обладает высочайшей теплопроводностью.
Аналогичные подходы с переходом одного вида энергии в другой относятся и к ядру атома- нуклонам, с одной лишь разницей: переход электрона из материальной частицы в электромагнитный импульс и наоборот происходит в интервале температур и частот, доступных для измерения в условиях сегодняшнего уровня науки и техники- 60000≥Т (градус)≥1, а преобразования в нуклонах за пределами этих температур — 6×10⁷≤ Т (градус)≤1х10^-3 .
Итак, автором приняты два предположения:
1. 2n²/z — количество квант-состояний электрона
(группы);
2. Электрон имеет условия, при которых он переходит из материальной частицы в электромагнитный импульс (что объясняет так называемый дуализм).
В продолжение рассуждения, для атома водорода с зарядом ядра z=1 (¹₁H) количество 2n²/z принимает значение 2n². Следовательно, у водорода на одиннадцатой электронной оболочке 2n²= 2 • 11²= 242 квант-состояний электрона. Но это, как трактуют учебники, всего лишь количество электронов (квант-состояний электронов) на одиннадцатой оболочке. Но каждая из одиннадцати оболочек также квантуется по энергетическому потенциалу по формуле Е_n = Е/n²(общепринятая формула).
На первой электронной оболочке у атома водорода (¹₁H) в отличии от гелия (⁴₂He) только один электрон, и соответственно, у водорода на первой оболочке должно быть два квант-состояний электрона. В учебниках же, да и на практике, при расчетах применяют формулу Е_n = Е/n² что является верным для гелия (⁴₂He) в матрице «121 х 121» (об этом ниже), но для водорода указанное будет не верно. Расчёт квант-состояний у гелия 2n²/z = 2n²/2 = n², a у водорода 2n²/z = 2n²/1 = 2п², т.е. для водорода формула должна иметь вид Е_n = Е/2n² — водородная группа ¹₁H — водород; ²₁H — дейтерий; ³₁H — тритий — в матрице «242 х 242» (об этом ниже). Думаю, что именно по этой причине (см. нижеприведённые расчёты) и отсутствует взаимосвязь λ и ν — длины волны и частоты излучения от температуры, при которой до настоящего времени в учебниках по физике λ • ν ≠ с (с = 3 • 10 ⁸ м/с).
Итак, с первой по одиннадцатую оболочки у атома водорода ( H¹₁) будет En = E/2n² = Е/2•11²= Е/2•121 = Е/242 энергетических квант-состояний.
В результате имеем Е/242 = 242Wn – двести сорок два энергетических квант-состояний электрона с первой по одиннадцатую оболочки, и 2n² = 242 квант-состояния электрона на самой одиннадцатой оболочке.
В результате имеем Е/242 = 242W_n — двести сорок два энергетических квант-состояний электрона с первой по одиннадцатую оболочки, и 2n² = 242 квант-состояния электрона на самой одиннадцатой оболочке.
В целом мы имеем 2n² х 2n² =242 х 242 = 58564
квант-состояний электрона у атома водорода (¹₁H).
У атома гелия эта схема будет выглядеть как 2n²/z х 2n²/z = n² х n² = 121 х 121 = 14641 квант-состояний группы электронов (группа из двух электронов).
Следовательно 2n²/z x 2n²/z — количество квант-состояний электронов (группы электронов z) у любого атома с зарядом ядра «z». Причём, первый сомножитель 2n²/z — квант-состояния потенциала с первой по одиннадцатую оболочки, второй сомножитель 2n²/z -квант-состояние электрона на самой одиннадцатой оболочке.
Именно такой подход будет взят за основу для согласования параметров любых атомов таблицы Менделеева между собой, т.е. попробуем создать «единую систему координат». Схему определения квант-состояний для водорода «242 х 242» и гелия «121 х 121» назовём матрицами (2n²/z x 2n²/z — матрица).
Эти матрицы квант-состояний электрона (групп электронов) представлены на прилагаемых фигурах, где:
на фиг. 1 представлена матрица «242 х 242»;
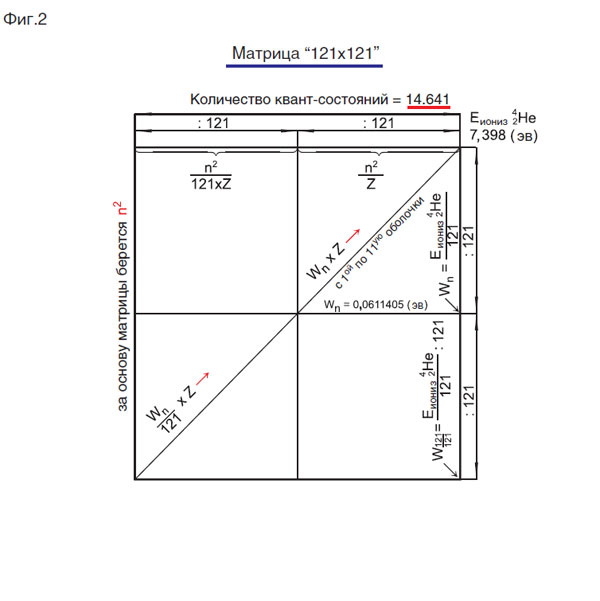
на фиг. 2 — матрица «121 х 121»;
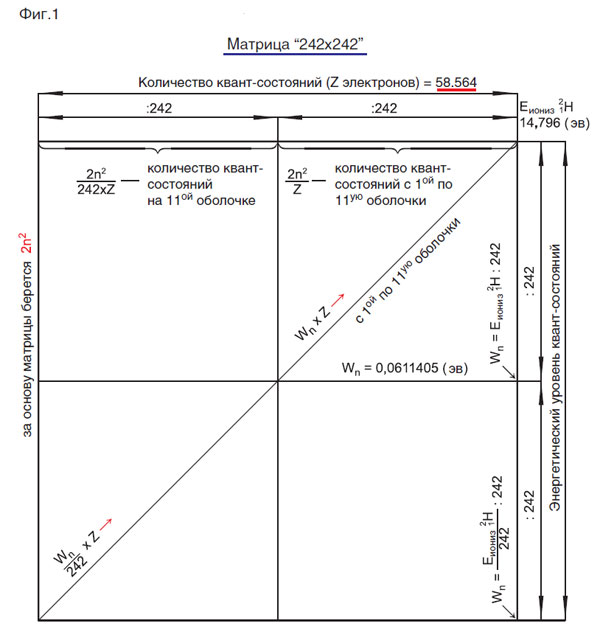
на фиг. 3 — совмещённые матрицы, при этом из фиг. 3 видно, что количество квант- состояний матрицы «242 х 242» равно 58564, что в четыре раза превышает «размеры» или количество квант- состояний матрицы «121 х 121»; действительно — 58564 / 14641 = 4.

Есть и другой приемлемый способ, позволяющий как бы развернуть электронные оболочки атома и представить их в виде дуги. При этом матрица будет отражать не количество квант-состояний электров (групп электронов) в целом, а квантование два раза, первый раз с первой по одиннадцатую оболочки, второй- на самой одиннадцатой оболочке. Т.е. мы можем преобразовать матрицу 2n²/z = n²/z + n²/z, что значительно упростит понимание происходящих процессов при выборе «единой системы координат» для расчётов параметров атомов и увязки их характеристик между собой. Вид преобразованной матрицы «121 х 121» (она может быть и «121×121» и «242 х 242») представлен на фиг. 4.

Наиболее универсальным атомом по отношению ко всем другим является атом гелия с матрицей «121 х 121». Поэтому, выбирая «единую систему координат» берём за основу схему квантования гелия.
В результате предыдущих рассуждений мы пришли к выводу, что 2n²/z можно представить не просто как количество электронов на n-ой оболочке, а как
— (2n²/z) — количество квант-состояний электрона (групп электронов) атома с зарядом «z» (см. фигуры 1 и 2),
— 2n²/z = n²/z + n²/z — развёрнутые (по дуге) оболочки атома, где происходит двойное квантование.
Первый раз с первой по одиннадцатую оболочки, второй — на самой одиннадцатой оболочке (см. фиг. 4).
Забегая вперёд необходимо отметить, что именно при повторном квантовании на одиннадцатой оболочке и происходит переход электронов из материального состояния (частицы) в энергетическое (электромагнитный импульс). Одиннадцатая оболочка любого атома является показателем резонансных характеристик или резонансным квант-состоянием атома. Именно на одиннадцатой оболочке создаются условия для появления 2m_eс², 4m_eс², 8m_eс².
Для расчётов применим формулы и const, используемые на практике. Первоначально, установим причину несоответствия зависимостей частоты и длины волны от температуры. Для этого обратимся к формулировкам и толкованиям закона смещения Вина:
— частота, соответствующая максимальному значению спектральной плотности энергетической светимости чёрного тела, пропорциональна его термодинамической температуре;
— длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости чёрного тела, обратно пропорциональна его термодинамической температуре.

Для устранения последнего несоответствия или его объяснения проводились дальнейшие исследования вида функции Кирхгофа.
Формула Рэлея-Джинса хорошо согласовалась с данными опытов только в области малых частот излучения. Для больших частот она была явно неверна.
Невозможность отыскать такое выражение для функции Кирхгофа, которое согласовывалось бы с данными экспериментов во всём интервале частот от «0» до бесконечности, получило образное название «ультрафиолетовой катастрофы». В 1910 году М.Планку удалось найти вид функции частоты от температуры, в точности соответствующей опытным данным, введя понятие порций энергий (квантов). Постоянной Планка называют коэффициент пропорциональности h между энергией Е и частотой v: Е = hv.

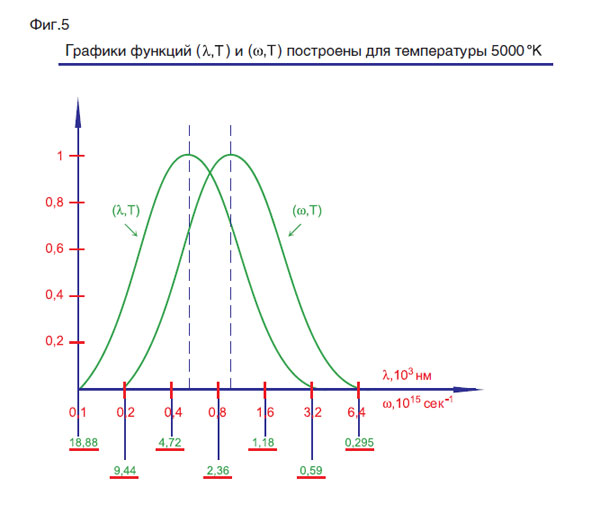
Решение вопроса, почему функции (w,Т) и (λ,Т) при одной и той же температуре не связаны соотношением λ = c/v, является звеном цепи, позволяющим ответить и на многие другие вопросы.
Итак, помимо взятых за основу предыдущих предположений:
— 2n²/z = n²/z + n²/z -двойное квантование, при
котором второе квантование происходит на одиннадцатой оболочке (см. фиг. 4);
— (2n²/z)² — количество квант-состояний электрона (групп электронов) атома с зарядом ядра «z»,
(2·121/1)·(2·121/1) = 242 х 242 = 58564 — для водорода
(2·121/2)·(2·121/2) = 121 х 121 = 14641- для гелия

— «матрицу квантования» выбираем «121 х 121» соответствующую гелию;
Введём ещё два предположения, руководствуясь следующим:
Вводя «единые координаты» для всех атомов (матрица «121 х 121»), обратимся к формуле, определяющей энергию электрона в электростатическом поле ядра:

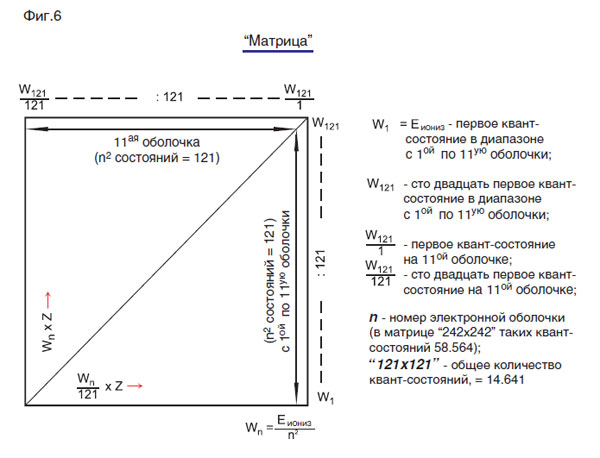
Упрощённая матрица двойного квантования представлена на фиг. 6, где с первой по одиннадцатую оболочки квантуются только W_n = Е/n² , а на самой одиннадцатой оболочке- потенциал одиннадцатой оболочки (W_n/121):121; W₁ = Е_иониз— первое квант-состояние в диапазоне с первой по одиннадцатую оболочки; W121 — сто двадцать первое квант-состояние в диапазоне с первой по одиннадцатую оболочки; W₁₂₁/I-первое квант-состояние на одиннадцатой оболочке; W₁₂₁ — сто двадцать первое квант-состояние в одиннадцатой оболочке; n — номер электронной оболочки.

Поскольку у водорода 58564 квант-состояний электрона, определим потенциал, приходящийся на одно квант-состояние. Обозначим эту величину «Ш» универсальная постоянная:
Ш = 13,619 : 58564 = 2,32549 · 10^-4 эВ или
Ш = 2,32549 · 10^-4 эВ на квант-состояние.
Зная, что у водорода при n = 1 частота v = R = 3,2931193 · 10¹⁵ с^-1, определим значение частоты у водорода, приходящейся на одно квант-состояние. Обозначим полученную величину «М» — универсальная постоянная:
М = 3,2931193- 10¹⁵: 58564 = 562,31119·10⁸ Гц
или
М = 562,31119 · 10⁸ Гц на квант-состояние. Зная частоту одного квант-состояния водорода, рассчитаем и длину волны, приходящуюся на одно квант-состояние электрона:

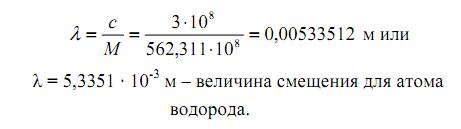
Но из закона смещения Вина, постоянная Вина b = 2,898 ·10^-3 м · Кº, причём это значение точно соответствует практическим результатам.
Порядок цифр, полученный при наших расчётах по водороду — 5, 3351 · 10^-3 м и постоянная Вина b = 2,898 · 10^-3 м · Кº, т.е. разница в этих значениях позволяет предположить, что постоянная Вина относится не к атому водорода, а к атому гелия.
Перейдя в этой связи к расчёту атома гелия, первоначально выполним следующее.
Пересчитаем постоянную Вина b = 2,898 · 10^-3 м · Кº в частоту λ · Т= 2,898 · 10^-3 м · Кº:

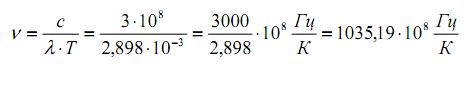
Поскольку у гелия 14641 квант-состояний, то максимальное значение v (при условии, что одно квант-состояние принимаем за 1º К ) будет равно:
1035,19 · 10⁸ · 14641 = 15156216 · 10⁸ или
vmax= 15156216- 10⁸Гц/К.
У гелия как и у водорода в единой системе координат (в матрице «121 х 121») максимально возможное значение vmax может принимать значение vmax = R / (Т · n (квант-состояний)), где R = 3,2931193 · 10¹⁵ с^-1 делённое на одно квант-состояние температуры. Тогда одно квант-состояние температуры для гелия будет равно:

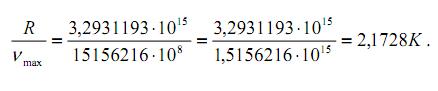
Т.е. у атома гелия на одно квант-состояние (двух электронов) приходится 2,1728 К, при этом отметим, что у водорода на одно квант-состояние приходится одна единица.
Подытожим полученные результаты:
а) величина смещения у водорода «λ¹₁H» = 5,3351 · 10^-3м; величина смещения Вина у гелия «λ⁴₂He» = 2,898 · 10^-3м · Кº;
б) частота на квант-состояния у водорода «М ¹₁H» = 562,311 · 10⁸Гц; частота на квант-состояния у гелия «М ⁴₂He» = 1035,19 · 10⁸Гц/Кº;
в) величина одного квант-состояния у водорода — одна единица;

Сопоставив единицы измерения в выражениях по водороду и гелию, приняв во внимание, что порядок цифр соразмерен, мы имеем право допустить, что к единицам измерения по водороду так же, как и у гелия можно выражение (название единиц измерения) соотнести к градусу Кельвина. Тогда, на одно квант-состояние по водороду, мы получим const:
Ш = 2,32549 · 10/^-4эВ/К; М = 562,31119 · 10⁸ Гц /К;
одно квант-состояние = 1 °К.
Приняв во внимание, что одно квант-состояние у атома водорода равно 1 °К, а всего у водорода 58564 квант-состояний, получим, что максимальная температура атома водорода, соответствующая температуре ионизации будет равна 1 · 58564 = 58564 °К или T_иониз¹₁H=58564K°

У гелия одно квант-состояние равно 2,1728 °К и в наличии 14641 квант-состояний. Соответственно температура ионизации составит 2,1728 · 14641 = 31812 °К или T_иониз⁴₂He=31812K°
Следует обратить внимание на тот факт, что последняя электронная пара у гелия (последнее квант-состояние) имеет потенциал 2,1728 К, соответственно, ниже этой температуры электроны отсутствуют (они переходят из состояния материальной частицы в энергетическое состояние) — это и является причиной сверхтекучести гелия II рода. Здесь происходит, так называемое, фазовое изменение гелия. Гелий I рода переходит в состояние гелия ІІ рода.
Исходя из того, что по представленным расчётам последнее квант-состояние, при котором у гелия ещё имеются электроны- при температуре 2,1728 К, а ниже этой температуры электроны как таковые отсутствуют, и совпадение этого уровня температуры с практическими результатами, при которых (ниже 2,1728 К) гелий переходит в сверхтекучее состояние, мы имеем право сделать заключение, что наши рассуждения и подход к взаимосвязи гелия и водорода являются правильным.
Более того, такое объяснение сверхтекучести гелия является наиболее объективным и понятным с точки зрения здравого смысла. Ведь при отсутствии электронов, атом гелия становится просто ядром (в материальном понимании), а, соответственно, любой может подсчитать, во сколько раз меньше стал диаметр материального ядра по сравнению с диаметром атома гелия- когда присутствуют электроны даже на первой оболочке, ни говоря уже о третьей, пятой и т.д.! Кроме того, что не менее важно, у нас появилось объяснение, почему постоянная смещения Вина b = 2,898 · 10^-3 м · °К, имеющая хорошие практические результаты, не согласовывалась с функцией частоты от температуры. Причина оказалась в том, что λ смещения определялась практически по гелию a v смещения- по водороду.

Соотношение параметров у водорода и гелия- температур, постоянных смещения, частот квант-состояний- всё соотносится как 1,8409. Отсюда можно сделать вывод, что и энергия ионизации водорода и гелия также соотносится с коэффициентом 1,8409.

Принимая во внимание, что у гелия заряд ядра в два раза больше, чем у водорода E_иониз2⁴He, должна также
уменьшиться в два раза, однако уменьшение составило только 1,8409 раза. Это связано с тем, что у водорода только один протон и отсутствуют нейтроны, а в ядре гелия два протона и два нейтрона. В этой связи разница 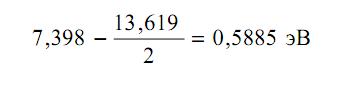объясняется наличием связи в ядре гелия двух дополнительных нейтронов.
Используем это обстоятельство для установления взаимосвязей атома водорода с его изотопами: дейтерием и тритием, а также связи между гелием и его изотопом.
Зная Е_иониз⁴₂Hе мы можем переходя к ядру с зарядом z = 1, т.е. к водороду, смело предположить, что у изотопа водорода дейтерия ²₁H, имеющего один протон и один нейтрон, потенциал Е_иониз²₁Hсоставит два потенциала Е_иониз⁴₂Hе, т.к. эти атомы абсолютно симметричны по составу ядер:

Разница в атоме водорода по сравнению с атомом дейтерия лишь в наличие у дейтерия
дополнительного нейтрона. Соответственно, один нейтрон у ядра с зарядом z = 1 даст изменение потенциала (увеличение) по сравнению с Е_иониз¹₁H водорода на 8,64234%.
Имеем право предположить, что у ядра с зарядом z = 2, два нейтрона буду изменять потенциал в большую сторону на 8,64234%. Попробуем проверить этот вывод: 6,8095эВ + 8,64234% = 7,398 эВ.
Этот подход может быть использован к любому ядру с зарядом z, но следует иметь в виду, что потенциал, относительно которого будет вестись отсчёт, определяется Е_иониз¹₁H/z, а количество нейтронов, которые будут давать приращение к потенциалу- 8,64234%- соответствует числу заряда атома z!
Произведём расчёт ещё одного изотопа водорода-трития ³₁H.
Рассчитаем его Е_иониз:
Зная Е_иониздейтерия, 14,796 эВ, нам достаточно увеличить этот потенциал на 8,64234% и получим Е_иониз трития 16,07472 эВ.
Захват дейтерием, ядро которого состоит из одного протона и одного нейтрона, ещё одного нейтрона вполне вероятен, т.к. масса ядра дейтерия превышает массу нейтрона почти в два раза.
Но нельзя исключать и случая, когда два нейтрона одновременно «попадают в объятия» атома водорода. Тогда тоже может образоваться изотоп трития, но уже с другим потенциалом.